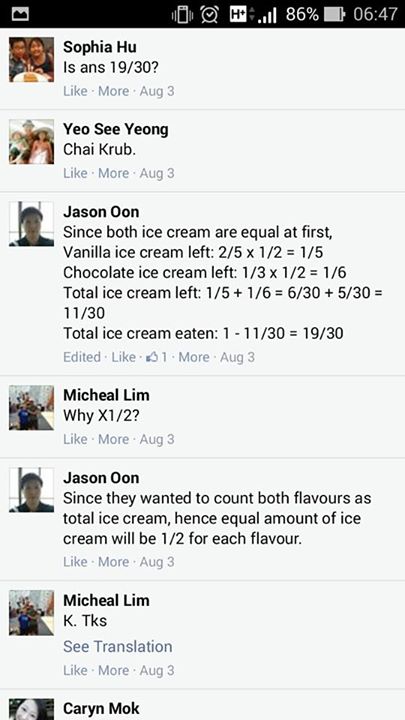
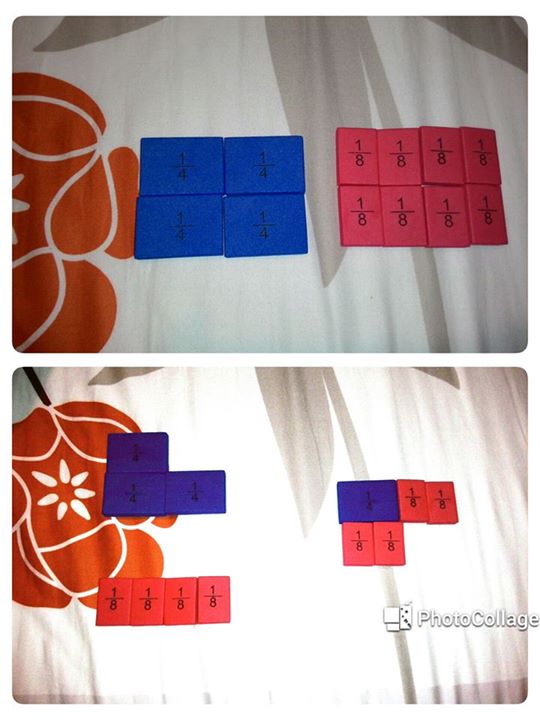
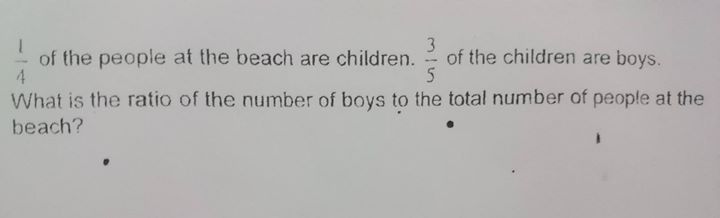Hi, I hope to get some opinions and answers to this P3 qn from my boy's sch. My boy has mistaken between "eaten" and "left". So I thought his answer should be 3/8 instead of 5/8. But his teacher explained that the answer shd simply be 1/2 + 1/4 = 3/4. What do you guys think? My boy and I are completely confused. Thank you in adv! :)